Project
Introduction
When listening to tonal music, a feeling of a change of tension arises due to a progression of chords which are bearers of (centripetal as dominant, or centrifugal as subdominant) forces. This is created by the cadential progression of their tonal harmonic functions. The beginning of the increase of tension is created by a different chord after the tonic. The lowering of tension and the concluding feeling emerges more strikingly when a chord including an ascending seventh degree (as the ‘leading tone’) resolves to the tonic with the eighth/first (hence fundamental) degree in the highest voice of the melody (‘soprano’). It is stronger if, simultaneously, the lowest voice (‘bass’) proceeds by a fifth leap downwards from the fifth degree to the fundamental/first degree. If in the key/scale (modal or tonal), the natural minor second did not occur between the seventh and eighth (‘finalis’ or ‘tonic‘) degrees (not customary in older modal scales), composers began to raise the seventh note in the composition with an accidental to achieve an artificial leading note. Frequent and regular harmonic conclusions as resolutions from dominant to tonic, typical for tonal music (as opposed to the static process of modal music) are alternate by the growth of the tension when proceeding from tonic to subdominant (and any other degrees).
Sample output of the algorithm. Mondscheinsonate
The changes of tension proceed in waves of alternation, where intensifying tension (through the subdominant, tending towards the most dynamic of the dominant) gives way to a relaxation of the tension (with the ascending resolution of a leading tone, which has a tendency to advance) and to the final fundamental degree. All these forces, depending on the progressions of harmonic functions, can be found automatically?
We hope this software will help distinguish and characterize a composer´s style as his harmonic fingerprint according to his preference for the more common types of cadences in his compositions. The type of cadence is characterized in two dimensions:
- Quantitatively in the lengths of cadences based on the number of cadence steps, i.e. processing of various chords created on a different scale degree, where every cadence starts with a tonic (T) and ends with the next tonic.
- Qualitatively in the types of chords and their harmonic functions used in all of these cadence steps
The software detects, evaluates and counts cadences in two ways:
- By searching for an occurrence of pre-set cadences. These are cadences frequently used by other composers (i.e. T-S-D-T, T-II-D-T, T-S-T4/6,D-T, T-II-T4/6-D-T, etc.). Here might be every chord except T as a triad or seventh chord, for D also as a nonachord.
- By searching for all kinds of progressions of harmonic functions between the tonic and the next nearest tonic in the analysed composition, and in this way listing all the preferred progressions of cadences of the examined composer
Algorithm
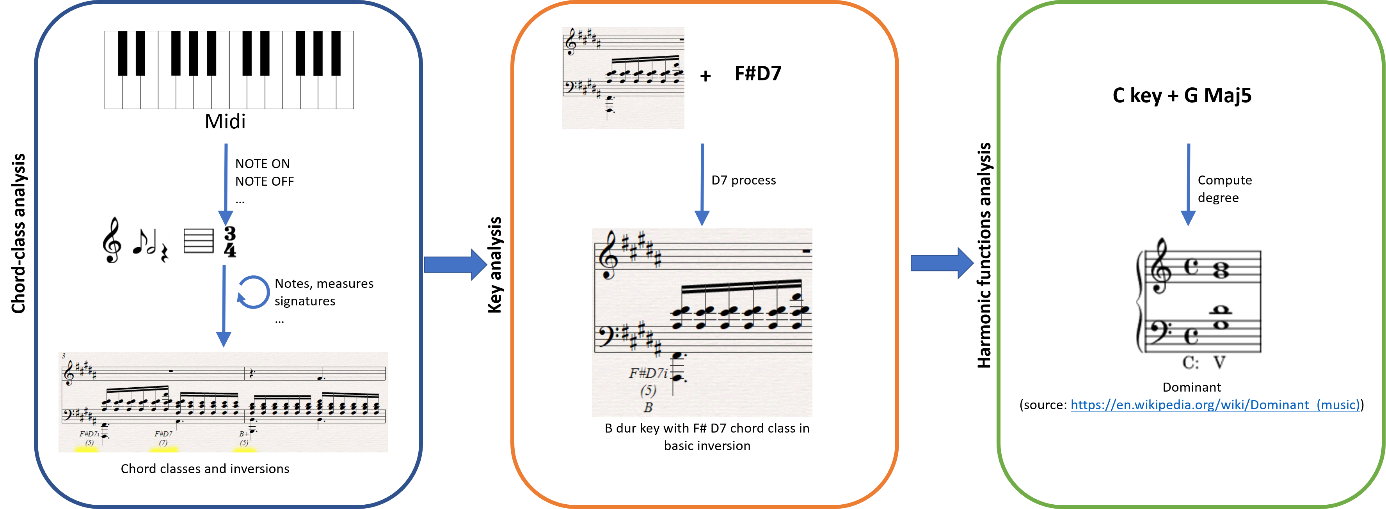
Using midi files as input, this algorithm detects and determines chord classes, the key (major or minor centre) and harmonic functions in a musical score. The process is undertaken in three layers and implemented in Java. The result can be viewed using the Sibelius plugin (Javascript), which is also part of the solution.
Layers:
- Chord-class analysis
- Reads the midi file and transforms it into a format allowing the program to work with higher level structures (measures, measure sections, beats, time and key signatur
- Each measure is read and possible structures of chords are found for both vertically and horizontally arpeggiated superpositions of thirds. They are compared against each other taking into consideration factors such as the weight of chord tones and probability. The elimination of melodic tones is performed taking into consideration beat length and the prevailing length of tones in the measure and whether they are not at a distance of a third from any of the other tones of the beat/simple measure.
- Each measure can be divided into simple measures (e.g. 6/8 time signature, into two groups of three 1/8 notes) for better chord detection. The program can divide a measure section into individual beats when needed
- Key analysis
- Uses results specified and collected by chord analysis with additional information from the score
- For a known key signature from the beginning (of a processed section), the major/minor key pair is found and confirmed or rejected by the corresponding major or minor chord
- The program then iterates over measure sections and reacts to the current chord and tone. For each situation, the program has a defined process which decides which key is present or if key cannot be detected and moves on
- A major/minor key pair are determined by certain chords, where we need to additionally confirm one of them and some chords helps to identify a key/scale directly
- For a known key during score processing, the same key can be assigned until a tone from the key is found. We then seek its confirmation (i. e. the tone is later repeated in a chord), or apply a known process that can determine the key
- If the key cannot be determined by the above processes, we can try to detect the scale by collecting the closest group of seven tones of neighbouring chords (after eliminating melodic tones), to see if they form a major/minor key/scale
- Harmonic functions analysis
- Utilises key and chord analysis results
- The tonal/harmonic functions are identified according to the scale degree of the root of each chord. This allows the determination of functions such as dominant and sub-dominant, etc. and gives us better data to discover cadencies, patterns and the style of the music in the score
- The third layer is being developed
Example
The example (from the Moonlight Sonata by L.v.Beethoven) shows the harmonic analysis results in the Sibelius output, as they are displayed under the bottom staff.

- The first character is for the harmonic function of the detected and analysed chord (T - tonic, S - subdominant, D - dominant, others only in Roman numerals as the scale degree) according to the degree of its root.
- The second Roman numerals in brackets are for the scale degree of the root of the chord in the detected tonal key,
- After the forward slash “/” is the Arabic numeral for the position of the triad (“/5” for the root position, “/6” for the 1st inversion, and “/4,6” for the 2nd inversion), or of the seventh chord: (“/7” for the root positions, “/5,6” for the 1st inversion, “/3,4” for the 2nd inversion, “/2” for the 3rd inversion).
- In the second row in square brackets is the name of the key. For a major key, there is a capital letter, for a minor key there is a lower case letter. The signs for shifted notes are traditional accidentals of # and b.
- The detected key of the beginning of the displayed music passage is C# minor, changed in the 4th bar of the example to E major